在多通道成像的时候，由于各种原因可能存在需要配准的情况。这里介绍一种最简单的刚性配准方式。

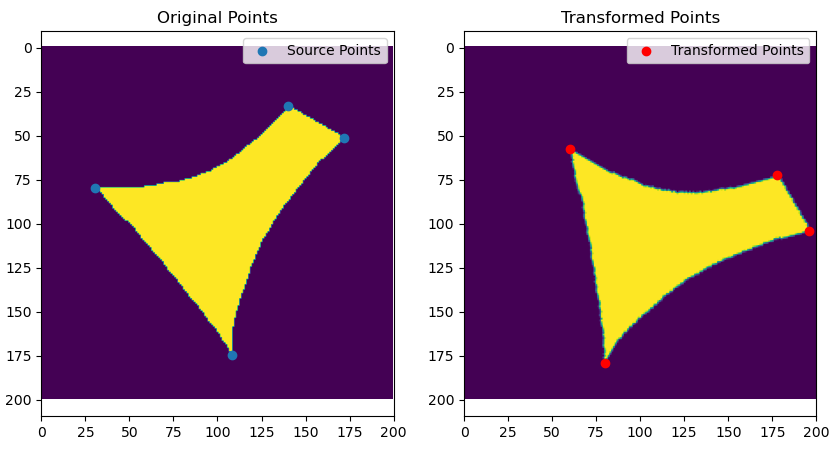
首先，在 ImageJ 中，使用 MultiPoint选择工具，将两个通道的图像中相匹配的特征点（比如多色荧光小球的信号点）选中，然后分别保存它们的ROI记录。在 python 中可以通过如下代码读取ROI记录并获取坐标：

import roifile
a = roifile.roiread("a.roi")
b = roifile.roiread("b.roi")
src = a.coordinates()
dst = b.coordinates()

然后通过下面的代码计算平面旋转矩阵和平移向量：

import numpy as np

def compute_rotation_translation(a_points, b_points):
    # 计算质心
    a_center = np.mean(a_points, axis=0)
    b_center = np.mean(b_points, axis=0)
    # 中心化处理
    centered_a = [point - a_center for point in a_points]
    centered_b = [point - b_center for point in b_points]

    # 构建H矩阵
    H = np.zeros((2, 2))
    for a, b in zip(centered_a, centered_b):
        outer_product = np.array(a).reshape(-1, 1) @ np.array(b).reshape(1, -1)
        H += outer_product
    # SVD分解
    U, _, Vt = np.linalg.svd(H)
    # 计算从a到b的旋转矩阵R，并确保行列式为1
    R = Vt.T @ U
    det_R = np.linalg.det(R)
    if not np.isclose(det_R, 1.0):
        Vt[1] *= -1
        R = Vt.T @ U
    # 计算从a到b的平移向量t
    t = b_center - R @ a_center
    return R, t

R, t = compute_rotation_translation(a_points=src, b_points=dst)

对于普通用户，旋转矩阵可能并不直观，可以通过以下方法转换为角度：

assert (np.linalg.det(R)-1)<1e-3
# 旋转矩阵的行列式为1，则为纯旋转矩阵，此时才能计算角度，否则需要归一化。
# 计算角度。默认是从a到b顺时针
angle_radians = np.arctan2(R[1, 0], R[0, 0])
angle_degrees = np.degrees(angle_radians)
print(f"旋转角度：{angle_degrees}度")

然后是基于计算出来的旋转矩阵和平移向量，构建仿射变换矩阵，并应用于图像a，使之与b对齐：

import cv2

M = np.array([[R[0][0], R[0][1], t[0]],
              [R[1][0], R[1][2], t[1]],
              [0,0,1],
              ])
img_A = cv2.imread('a.tif')
img_B = cv2.imread("b.tif")
img_A_aligned = cv2.warpAffine(img_A, M[:2], (img_A.shape[1], img_A.shape[0]))

# 将两个图像水平拼接查看变换情况。
combined = np.hstack((img_B, np.ones(img_A.shape), img_A_aligned))
plt.imshow(combined)
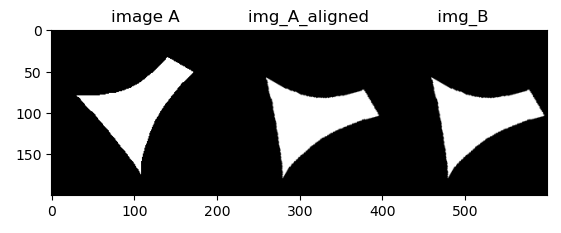
plt.show()

结果如下：