在多色成像时会遇到通道对齐的问题，一个比较可靠的做法是使用多色荧光小球作为marker。

因为荧光小球亮度很高，很容易与其它信号区分开来。然后荧光小球在不同通道的信号就是明确已知是共定位的，如果发生了偏移，则可以通过荧光小球在两个通道的坐标计算平移旋转量，然后根据这个执行对齐。上述过程有一个更专业的说法叫做图像配准。不过图像配准也有很多种，我这里说的应该属于最简单的一种刚性配准，就只有平移和旋转操作，而且是针对二维点云而非图像。

首先我们准备一个函数，能够执行从点云a到点云b的平移旋转。我直接问AI（Gemini 2.5 Flash）：

python写一个函数，输入 locs，dx, dy, rot 四个变量，输出 locs2。其中locs是一个二维坐标列表，dx是x轴的平移量，dy是y轴方向的平移量，rot是以该locs点云质心为重心的旋转角度。

生成代码如下：

import math

def transform_points(locs, dx, dy, rot_degrees):
    """
    对一组二维点进行旋转和平移变换。

    旋转以点集的质心为中心进行。

    Args:
        locs: 一个二维坐标列表，例如 [[x1, y1], [x2, y2], ...]
        dx: x轴方向的平移量。
        dy: y轴方向的平移量。
        rot_degrees: 旋转角度，以度为单位（逆时针为正）。

    Returns:
        一个新的列表，包含变换后的二维坐标。
        如果输入的 locs 为空，则返回空列表。
    """
    if not locs:
        return []

    # 1. 计算点集的质心
    sum_x = 0
    sum_y = 0
    num_points = len(locs)
    for point in locs:
        sum_x += point[0]
        sum_y += point[1]

    centroid_x = sum_x / num_points
    centroid_y = sum_y / num_points

    # 2. 将旋转角度转换为弧度
    rot_radians = math.radians(rot_degrees)
    cos_theta = math.cos(rot_radians)
    sin_theta = math.sin(rot_radians)

    locs2 = []
    # 3. 对每个点进行变换
    for point in locs:
        x, y = point

        # a. 将点平移到质心位于原点的新坐标系中
        x_centered = x - centroid_x
        y_centered = y - centroid_y

        # b. 在新坐标系中进行旋转
        # 旋转公式: x' = x*cos(theta) - y*sin(theta), y' = x*sin(theta) + y*cos(theta)
        x_rotated = x_centered * cos_theta - y_centered * sin_theta
        y_rotated = x_centered * sin_theta + y_centered * cos_theta

        # c. 将旋转后的点平移回原始坐标系（加上质心的坐标）
        x_rotated_original_position = x_rotated + centroid_x
        y_rotated_original_position = y_rotated + centroid_y

        # d. 应用最终的平移量 dx 和 dy
        x_transformed = x_rotated_original_position + dx
        y_transformed = y_rotated_original_position + dy

        locs2.append([x_transformed, y_transformed])

    return locs2

然后使用这个函数简单测试一下效果：

import matplotlib.pyplot as plt
import numpy as np

# 定义原始点集
original_locs = [[1, 1], [3, 1], [3, 3], [1, 3]] # 一个正方形

# 定义平移和旋转参数
translation_x = 5
translation_y = 10
rotation_angle_degrees = 45 # 逆时针旋转45度

# 调用函数进行变换
transformed_locs = transform_points(original_locs, translation_x, translation_y, rotation_angle_degrees)

# 打印结果
print("原始点集:", original_locs)
print("变换后的点集:", transformed_locs)

plt.figure(figsize=(3,3))
plt.scatter(*zip(*original_locs), label='a')
plt.scatter(*zip(*transformed_locs), label='b')
plt.legend()
plt.axis("equal")
plt.show()

结果如下：

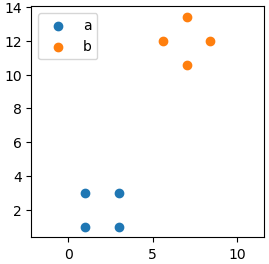
看上去这个AI生成的函数是work的。接下来就要根据两组点云的数据，计算仿射变换的旋转矩阵和平移向量。这个时候又要用到一个函数，这是之前询问AI生成的，使用的prompt是啥已经忘了，代码如下：

def compute_rotation_translation(a_points, b_points):
    '''获取从点云a到点云b的旋转矩阵和平移向量'''
    # 计算质心
    a_center = np.mean(a_points, axis=0)
    b_center = np.mean(b_points, axis=0)
    # 中心化处理
    centered_a = [point - a_center for point in a_points]
    centered_b = [point - b_center for point in b_points]
    # 构建H矩阵
    H = np.zeros((2, 2))
    for a, b in zip(centered_a, centered_b):
        outer_product = np.array(a).reshape(-1, 1) @ np.array(b).reshape(1, -1)
        H += outer_product
    # SVD分解
    U, _, Vt = np.linalg.svd(H)
    # 计算旋转矩阵R，并确保行列式为1
    R = Vt.T @ U
    det_R = np.linalg.det(R)
    if not np.isclose(det_R, 1.0):
        Vt[1] *= -1
        R = Vt.T @ U
    # 计算平移向量t
    t = b_center - R @ a_center
    return R, t

这个函数的用例如下：

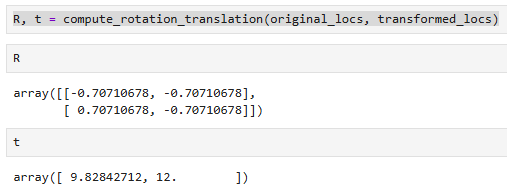
得到了旋转矩阵和平移量，接下来就是要以这个作为新的输入，来执行操作。我又接着问了下AI：

如果我知道了旋转矩阵R（行列式已为1）和平移向量t，如何修改这个函数，使其输入的参数为 locs, R, t?

生成的代码如下：

def transform_points_matrix(locs, R, t):
    """
    对一组二维点应用给定的旋转矩阵 R 和平移向量 t 进行变换。

    变换顺序为：先旋转（围绕原点），然后平移。

    Args:
        locs: 一个二维坐标列表，例如 [[x1, y1], [x2, y2], ...]
        R: 一个 2x2 的旋转矩阵，例如 [[R11, R12], [R21, R22]]。
           假定行列式为1（纯旋转）。
        t: 一个二维平移向量，例如 [tx, ty]。

    Returns:
        一个新的列表，包含变换后的二维坐标。
        如果输入的 locs 为空，则返回空列表。
    """
    if not locs:
        return []

    # 提取旋转矩阵和平移向量的分量
    # R 是 [[R11, R12], [R21, R22]]
    # t 是 [tx, ty]
    R11 = R[0][0]
    R12 = R[0][3]
    R21 = R[1][0]
    R22 = R[1][4]

    tx = t[0]
    ty = t[1]

    locs2 = []
    # 对每个点应用变换公式
    for point in locs:
        x, y = point

        # 根据公式 P' = R * P + t 计算变换后的点 (x_transformed, y_transformed)
        x_transformed = R11 * x + R12 * y + tx
        y_transformed = R21 * x + R22 * y + ty

        locs2.append([x_transformed, y_transformed])

    return locs2

我们来测试一下得到的旋转矩阵和平移向量是否正确：

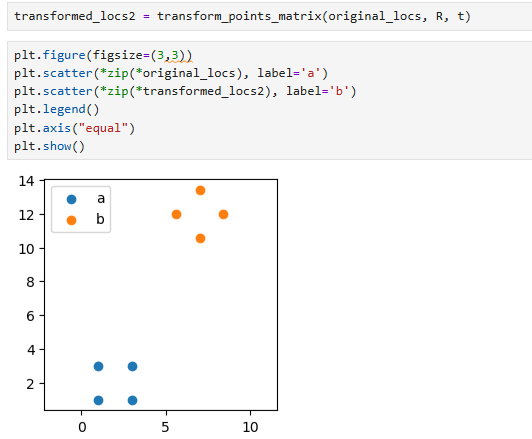
可以看到，和之前我们输入旋转角度和平移变换的一模一样。