通过阈值分割图像中的前景和背景是成像数据分析中基础的基础。此处以skimage.filters.threshold_li函数为例，介绍基于最小交叉熵的图像阈值搜索算法。

虽然我们可以通过ImageJ预览图像的像素直方图，并结合目视检查的情况，人为设定一个比较合理的背景阈值。但这样做只适合于少量数据分析。

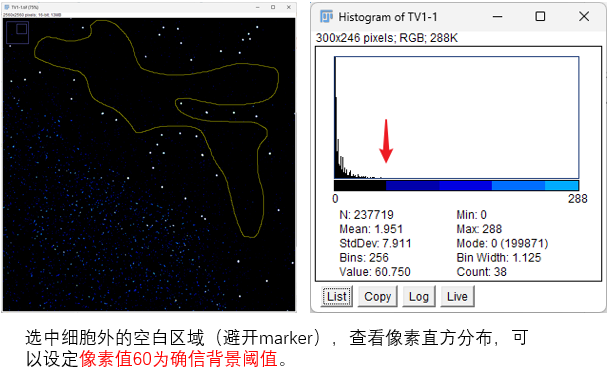
而且这样设定的阈值，依靠的是个人感官，所以只是一个估计值。所以为了阈值的设置更加科学，这里推荐使用以信息论为理论基础的 skimage.filters.threshold_li 来获得更准确的背景阈值。

这个函数通过多次迭代搜索阈值，每次迭代会计算原始图像和二值化图像之间的交叉熵，然后使这个交叉熵最小。

最小化交叉熵的直观意义在于，经过阈值分割后的图像（用类平均灰度表示）与原始图像在信息上的差异最小，从而保留了原始图像最多的重要信息，实现了最优的分割。

但需要注意，该方法容易陷入局部最优值，如果存在这种情况，可以尝试指定initial_guess（既可以是数值，也可以是自定义估计函数）。

为了更放心稳妥地使用这个函数，我查看了这个函数的源代码，发现：

1. 如果不设置initial_guess, 默认第一次迭代时 t_next 为图像均值。
2. 第一次迭代时 t_curr 最开始都是从负数开始的。
3. 代码中并没有直接计算交叉熵，而是通过推导的公式来更新 t_next： t_next = (mean_back - mean_fore) / (np.log(mean_back) - np.log(mean_fore))。这个让我看了直挠头，涉及到李氏方法。

由于这个函数是通过迭代的过程搜索阈值，所以我想着能否将这个迭代的过程作图可视化，帮助我判断这个函数的运行机制。在AI的帮助下，让它修改这个函数的源代码，得到一个新的函数 threshold_li_with_history，我进行了一些测试。结果如下：

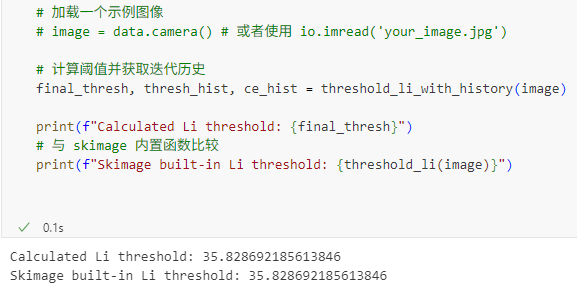
可以看到，交叉熵确实在下降，然后当前后两次交叉熵的差值小于设定的 tolerance 之后，搜索就结束了，函数范围当前的threshold。

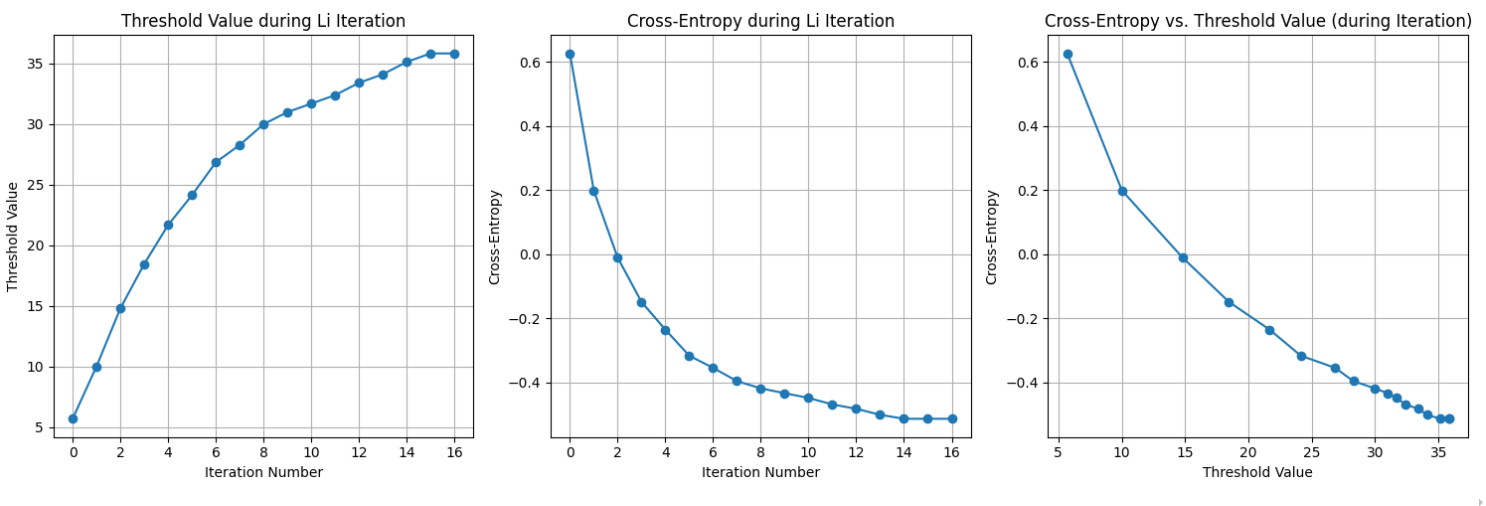
能够收集阈值搜索迭代历史的函数源代码如下：

绘制阈值搜索迭代历史的可视化代码如下：

# 绘制迭代过程中的阈值和交叉熵曲线
plt.figure(figsize=(15, 5))

# 绘制阈值随迭代次数的变化
plt.subplot(1, 3, 1)
plt.plot(thresh_hist, marker='o', linestyle='-')
plt.xlabel('Iteration Number')
plt.ylabel('Threshold Value')
plt.title('Threshold Value during Li Iteration')
plt.grid(True)

# 绘制交叉熵随迭代次数的变化
plt.subplot(1, 3, 2)
plt.plot(ce_hist, marker='o', linestyle='-')
plt.xlabel('Iteration Number')
plt.ylabel('Cross-Entropy')
plt.title('Cross-Entropy during Li Iteration')
plt.grid(True)

# 绘制交叉熵随阈值变化的曲线 (基于迭代过程中的记录)
plt.subplot(1, 3, 3)
plt.plot(thresh_hist, ce_hist, marker='o', linestyle='-')
plt.xlabel('Threshold Value')
plt.ylabel('Cross-Entropy')
plt.title('Cross-Entropy vs. Threshold Value (during Iteration)')
plt.grid(True)

plt.tight_layout()
plt.show()