对于很小的信号点比如单分子光斑，或者是单分子定位的散点cluster，我们可以忽略其本身的体积，视作质点来计算。这样可以计算质点之间的最邻近距离（Nearest Neighborhood Distance, NND），此时使用KDTree可以很好的解决问题。但是当信号是一个区域的时候，如果再使用NND，则单个cluster区域较大计算的质心NND就无法体现其分布聚集程度了。此时另外一个single particle level 的 metric 就是最小间隙长度。这是一个经典的“最近点对”问题，即寻找两个cluster中相邻最近的一对点。

都已经2025年了，谁还自己从头写代码啊。在 gemini 2.5 flash 的帮助下，我很快完成了这个功能的开发。首先我把自己的需求按照函数文档的框架组织好后告诉AI。这种写代码的方式我称之为函数文档式编程。

我有一个三维的成像数据，已经做好了图像分割，得到了它的label图像，label为0的是背景，label大于0时是分割后对象的索引标签。现在要计算每个对象的最邻近距离。注意这里的最邻近距离是两个对象轮廓边界之间的最小间隙长度，而不是两个对象的几何中心的直线距离。把这个功能写成一个python函数，输入的就是 mask.tif，这个mask.tif 使用 skimage模块读取，然后输出的是一张pd.DataFrame，其中包含了以下列：
1. label: 表示分割对象的标签或索引，注意排除0
2. xc: 对象几何中心的x位置，注意 mask.tif 读取后的shape是(z, y, x)
3. yc: 对象几何中心的y位置
4. zc: 对应几何中心的z位置
5. d: 与该对象最邻近的（即间隙长度最小时）对象间隙长度
6. label2: 最邻近对象的label
7. xc2: 最邻近对象几何中心的x位置
8. yc2: 最邻近对象几何中心的y位置
9. zc2: 最邻近对象几何中心的z位置
10. xe1: 和最邻近对象间隙最短连线与该对象边界交点x坐标
11. ye1: 和最邻近对象间隙最短连线与该对象边界交点y坐标
12. ze1: 和最邻近对象间隙最短连线与该对象边界交点z坐标
13. xe2: 和最邻近对象间隙最短连线与最邻近对象边界交点x坐标
14. ye2: 和最邻近对象间隙最短连线与最邻近对象边界交点y坐标
15. ze2: 和最邻近对象间隙最短连线与最邻近对象边界交点z坐标

AI很快就给我生成了可用的函数，并且附带了一个简单的测试案例，但是我觉得测试案例过于粗糙，不便于我检验。所以我又继续对测试代码的可视化部分功能提出要求：

请给上述代码中的示例补充三维作图可视化以便于我检验函数功能是否正确。要求：
1. 不同的对象使用不同的颜色，并添加其label作为文字标注。
2. 对象绘制绘制surface而不是散点，且surface要半透明。
3. 绘制最短间隙的连线。

AI又增加了可视化的函数，我看了下效果，虽然细节上有些问题，我对示例数据稍作修改，就充分满足了此次的分析需求。效果如下：

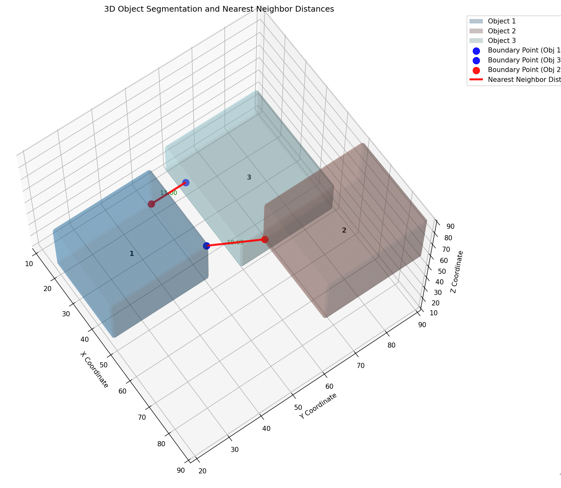
经过整理的完整代码如下：

看到这个AI（Gemini 2.5 Flash）现在这么强，我又继续尝试了其它一些AI，发现Gemini-2.5 Pro 也能生成满足需求的函数代码，但是思考时间太长。然后 Grok表现是让我最满意的，不仅代码看上去很简洁，而且三维可视化的时候效果更好（如下图）。但可惜的是，国内的 Qwen 和 Deepseek 生成的代码都是无法运行的。